Chapter
22 Printable One-Page Review
Understanding Profit
View Entire Chapter
with videos
B. Understanding profit requires bringing revenue and costs
together.
C. Demand determines marginal revenue.
1. Marginal revenue (MR) is the change in total revenue received from selling one more unit.
2. Demand may be thought of as average revenue with what is happening on the margin
an indication of what is happening to the average.
3. When product demand is down sloping, marginal revenue is below demand indicating
the average is going down.
4. The special case of horizontal perfectly elastic demand will be explored in chapter 23.
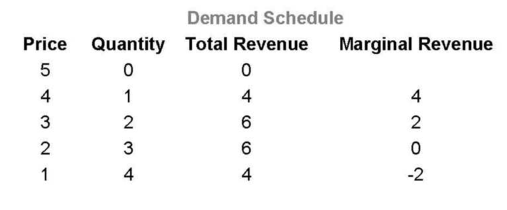
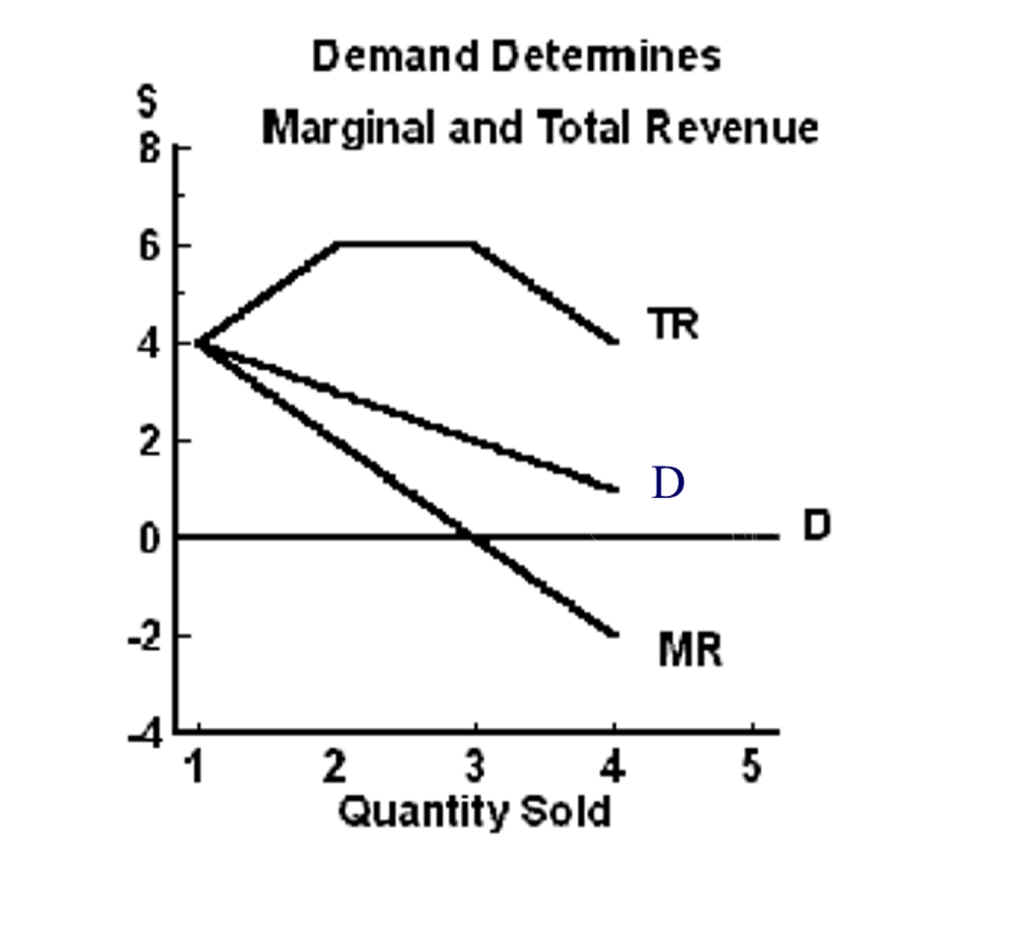
At high prices, demand is inelastic, lowering
price increases total revenue as marginal revenue is positive.
At medium prices, unitary elasticity means no
change in total revenue as price is changed.
At low prices, demand is elastic, lowering price
decreases total revenue as marginal revenue is negative.
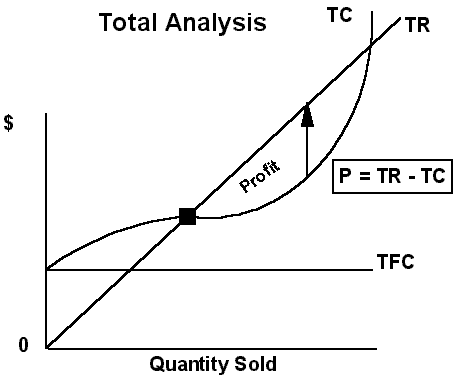
A. Selling quantity Q will maximize profit.
B. At quantities below optimum point Q, MR exceeds
MC and increasing quantity sold will increase profit.
C. At quantities above point Q, MC exceeds MR and an
increase in quantity sold will decrease total profit.
D. Maximum profit results when MR = MC
E. To find total revenue (TR) draw a perpendicular line
from the intersection of MR and MC to the quantity
axis. Then extend the line up to the demand curve
and over to the y-axis. The resulting rectangle is
P x Q which equals total revenue.
F. To find TC draw a line from the intersection of the
perpendicular and ATC to the y-axis. The resulting
rectangle is ATC x Q which is total costs.
G. The resulting top rectangle is TR-TC. It is total profit.
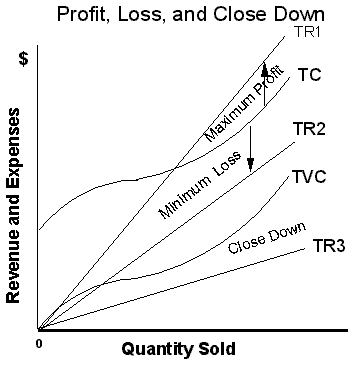
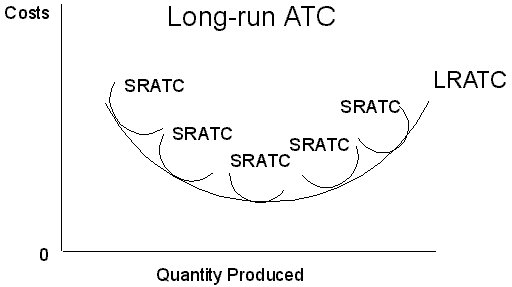affect profit Long-run costs Long-run average total costs
are the horizontal summation of ever larger short-run average total costs.